Estatística Prática para Docentes
e Pós-Graduandos
de Geraldo Maia Campos
18. Mudança de variável (exemplos
reais)
Neste texto, já foram comentados, em capítulos
anteriores, as transformações simples a que se podem submeter
os dados experimentais, visando a normalizar a distribuição
dos erros amostrais e a homogeneizar as variâncias, com a finalidade
de tornar possível a aplicação da estatística
paramétrica.
Todavia, o que, no presente capítulo, é
chamado de mudança de variável, são transformações
mais profundas e mais complexas, que não têm quaisquer regras,
fórmulas ou modelos fixos de transformação, como seria
o caso, se a transformação fosse logarítmica, raiz
quadrada, angular, ou qualquer das já comentadas anteriormente neste
texto.
Na verdade, a mudança de variável
é um recurso que se aplica a cada caso, individualmente, variando
conforme a natureza de cada experimento. São artifícios técnicos
da mesma natureza dos célebres artifícios de cálculo
usados em Matemática para resolver certos problemas, os quais só
valem para aquele determinado problema em pauta, ou, quando muito, para
problemas semelhantes.
Os exemplos que seguem não são hipóteses,
mas são todos recursos já empregados de fato pelo autor destas
páginas, para resolver problemas específicos e reais, de
pesquisadores diversos, que o procuraram em busca de auxílio.
Exemplo no.1: retas diferentes, como variável.
Um desses artifícios já foi citado
no capítulo anterior, quando se comentou o emprego dos parâmetros
da linha reta como variáveis. Já utilizei esse tipo de mudança
de variável, quando fiz o tratamento estatístico de uma tese
em que os dados experimentais eram medidas de densidade óptica feitas
em radiografias tomadas de um penetrômetro de alumínio apoiado
sobre o filme radiográfico.
Esse dispositivo (penetrômetro) tem forma
de escada, na qual os degraus tem espessuras crescentes, aumentando dois
milímetros em cada degrau ascendente. A imagem radiográfica
dessa escada de alumínio é uma série de faixas com
radiopacidade proporcional à espessura de cada degrau, cuja densidade
óptica é então medida em aparelho adequado a essa
finalidade.
A dificuldade, nesse tipo de trabalho, é
que uma radiografia não mostrava apenas um valor numérico,
mas vários, cada qual correspondente à densidade óptica
de um degrau do dispositivo. Parecia impossível tratar estatisticamente
os dados numéricos obtidos.
O artifício que tornou possível a
análise estatística envolveu algumas etapas, que passarei
a comentar, apenas para ilustrar a maneira como funcionou o raciocínio
do estaticista num caso como esse.
O primeiro passo foi realizar um teste de regressão
para múltiplas curvas, a fim de determinar qual a curva matemática
capaz de descrever a variação da densidade óptica
nos oito ou nove degraus do penetrômetro utilizado nos experimentos.
Ficou esclarecido assim que, naquele caso específico,
a curva era uma hipérbole de primeiro ou segundo grau (já
não me lembro), traduzida pela equação matemática
y = 1 / (a + bx) (hipérbole de primeiro grau), ou então y
= 1 / (a + bx)² (hipérbole de segundo grau). O segundo passo
foi realizar uma transformação hiperbólica dos dados,
que consistia em utilizar o inverso do valor dos dados experimentais (1/y,
no caso da hipérbole de primeiro grau, ou então 1/*y, no
caso da hipérbole de segundo grau), e não o valor original
(y).
Após essa transformação, um
novo teste de regressão mostrou que a relação entre
x e y era agora uma linha reta crescente da esquerda para a direita, o
que já era matematicamente de se esperar.
De fato, considerem a relação que
traduz a transformação hiperbólica de primeiro grau:
y = 1/(a+bx).
Se invertermos a posição de y e (a+bx),
o que resulta é sem dúvida uma linha reta: a+bx (linha reta)
= 1/y.
No caso da hipérbole de segundo grau, ocorre
o mesmo: y = 1/(a+bx)².
Invertendo-se as posições de y e (a+bx)²,
tem-se: (a+bx)² (parábola) = 1/y
Finalmente, extraindo-se a raiz quadrada de ambos
os membros da equação, tem-se:
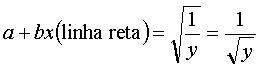
Essas operações algébricas mostram
claramente que, se for utilizado o inverso do valor do dado, em lugar do
dado original, a linha de regressão será indubitavelmente
uma reta, e não mais uma hipérbole de primeiro grau. Da mesma
forma, o uso do inverso da raiz quadrada do dado original transforma uma
hipérbole de segundo grau numa linha reta.
Mas qual seria a importância disso no caso
das radiografias? A importância está em que se pode mudar
a variável original (densidade óptica) e utilizar os dois
parâmetros (a e b) que definem a reta de regressão de cada
radiografia como duas novas variáveis.
A primeira delas, o parâmetro a da equação
da reta, traduz a densidade óptica de fundo da radiografia, ou seja
a densidade óptica do filme na região não interceptada
pela presença do penetrômetro. Graficamente, seria o ponto
onde a reta corta o eixo das ordenadas das coordenadas cartesianas, onde
x (espessura do degrau da escada de alumínio) é igual a zero.
E o parâmetro b nada mais é do que a tangente do ângulo
de inclinação da reta, ângulo esse que traduz radiograficamente
o grau de contraste do filme exposto.
De fato, se fizermos a = 0, o gráfico da
reta passará pela origem das coordenadas cartesianas, onde x e y
são iguais a 0 (zero). Essa reta, inclinada, formará com
o eixo horizontal um ângulo q,
cuja tangente será: tang q = y
/ x. Chamando a tang q de b, ter-se-ia:
b = y / x. Ou seja, a tangente do ângulo de inclinação
da reta é realmente o b da equação da reta. Isolando-se
o y, a equação ficaria assim: y = bx, sem o a, porque estamos
considerando que a reta passa por y = 0. Se y > 0, então a equação
terá de incluir o a, ficando assim: y = a + bx.
Essas duas novas variáveis, a e b permitiram,
portanto, estudar os filmes sob dois aspectos importantes em qualquer radiografia:
a densidade óptica geral e o contraste radiográfico dos filmes
(vencidos, não-vencidos, conservados ou não em geladeira,
armazenados ou não em estufas a 37/38 graus, para simular condições
ambientais favoráveis ou adversas à sua conservação.
Sem o artifício da mudança de variável,
de densidade óptica para os parâmetros a e b das diversas
retas de regressão, correspondentes a cada filme exposto, a análise
estatística dos resultados da pesquisa teria sido impraticável.
Exemplo no.2: associação de variáveis.
Contudo, a mudança de variável muitas
vezes pode ser utilizada também para diminuir o número de
variáveis de um trabalho de pesquisa, o que se consegue quando duas
ou mais dessas variáveis podem ser combinadas para dar origem a
uma outra variável, única, resultante dessa associação
entre duas ou mais delas.
Por exemplo, imagine-se um experimento em que se
desejasse saber qual, dentre uma série de soluções
solventes, seria a mais eficaz para dissolver uma determinada massa de
uma substância qualquer. O pesquisador poderia determinar a massa
(m) de cada corpo-de-prova (variável 1), medir o tempo (t) gasto
para a dissolução completa da massa correspondente a cada
um deles (variável 2), e calcular a velocidade de dissolução
(v), fornecida pela quociente massa dividida pelo seu correspondente tempo
de dissolução
— v = m / t (variável 3).
No entanto, essas três variáveis, que
exigiriam testes isolados para cada uma, poderiam ser associadas, resultando
numa variável única a ser analisada, que combinaria os efeitos
de todas as três.
Realmente, há na Física uma grandeza
que associa essas três variáveis: é a chamada Força
de Impulsão, definida pela expressão:F = m . v / t.
Mas o raciocínio matemático e físico
pode ir mais além.
De fato, partindo de três equações
da Física: uma que define a
Força (F = m . a), outra que define a velocidade de um móvel
(v = a . t), e finalmente a que define o Trabalho (T = F . e), nas quais
F = força, a = aceleração, m = massa, t = tempo, v
= velocidade, T = trabalho (ou energia despendida) e e = espaço
percorrido.
Podem fazer-se diversas transformações
algébricas simples: Se v = a . t, então a = v / t; e se a
= v / t e F = m . a, então F = m . v / t.
Contudo, m / t = v, e a equação ficaria
assim F = v . v, ou F = v².
Considerando, porém a equação
do trabalho (T = F . e), e tendo em mente que, no caso da dissolução
do tecido, o espaço percorrido (e) corresponde à massa dissolvida
(m), pode-se fazer a substituição do espaço pela massa
na equação do trabalho, uma vez que, nesse caso, e = m. Conseqüentemente,
T = F . m.
Substituindo agora, na equação T=Fm,
o valor de F, tem-se: T =m . v².
Como Trabalho e Energia são grandezas da
mesma natureza, uma vez que são avaliadas pela mesma unidade física
(Joule, erg), pode-se dizer indiferentemente: T=m . v², ou
E = m . v².
Finalmente, se a velocidade v fosse a velocidade
da luz (c), cairíamos na velha equação da liberação
da energia, descoberta por Einstein: E = m . c²!
Portanto, a nova variável de trabalho, calculada
a partir de variáveis medidas nos experimentos, seria agora a energia
(E) consumida na dissolução do tecido da polpa bovina, energia
essa que difere de uma para outra das soluções utilizadas
nos experimentos.
Exemplo: um massa de uma substância qualquer
com peso = 2,33g, dissolvida pela solução A em 53 segundos
teria uma velocidade de dissolução 2,33 / 53 = 0,044 g /
seg. A energia despendida, ou o trabalho realizado, nessa dissolução
seria
0,044² x 2,33 = 0,0045 ergs, ou, pelo SI (MKF) 45 x 10-7 Joules.
Em termos de Força, teríamos F = m
. v², ou F = 0,044², igual a 0,0019 dinas no sistema CGS, que
corresponde a 19 x 10-5 Newtons, aproximadamente, no sistema SI (MKF).
Ter-se-ia de multiplicar o resultado da operação por 9,80665,
mas a diferença é irrelevante para a análise estatística,
porque todos os dados seriam então multiplicados pelo mesmo valor
escalar.
Uma observação importante: após
a mudança das variáveis, a discussão dos resultados
da análise estatística terá forçosamente de
ser feita em termos da nova variável.
Exemplo no.3: a variável área (produto de 2 variáveis).
Imaginemos um trabalho de pesquisa em que se estuda
a velocidade de resfriamento de corpos-de-prova, deixados expostos ao meio
ambiente, após terem sido previamente aquecidos a temperaturas diferentes.
Para avaliar esse resfriamento, sua temperatura seria medida de minuto
em minuto, variando de um para outro corpo-de-prova.
Este tipo de pesquisa é um exemplo típico
de como se pode usar áreas como variável, em vez das duas
realmente utilizadas no decorrer do trabalho experimental, variáveis
essas que seriam o tempo gasto no resfriamento até a volta à
temperatura ambiente, e as medidas de temperatura do corpo-de-prova minuto
após minuto.
Lançadas em gráfico essas duas variáveis,
associadas como pares de tempo/temperatura, nos quais o tempo seria marcado
no eixo das abscissas (eixo de x), e as temperaturas nas ordenadas (eixo
de y), o resultado seria uma área fechada, limitada por três
linhas: duas retas (os eixos de x e y) e uma curva (curva de decrescimento
da temperatura ao longo do tempo).
As áreas determinadas por essas linhas podem
ser usadas como a variável do experimento, com a vantagem de associar
as duas variáveis utilizadas simultaneamente, e não isoladamente.
Essa nova variável traduziria numericamente a quantidade total de
calor perdido durante todo o tempo gasto no resfriamento dos corpo-de-prova.
Não se trata de uma sugestão puramente
teórica. Já usei pessoalmente esse recurso em um trabalho
de tese, para o qual os meus préstimos foram solicitados. No caso
real, registravam-se as temperaturas no interior de canais radiculares,
após a aplicação de irrigações com soda
clorada, e media-se, por meio de um par termoelétrico, a queda de
temperatura da solução, dentro do conduto, minuto a minuto,
durante o tempo decorrido até que a temperatura voltasse àquela
que o canal apresentava no início do experimento.
Às vezes, quando os erros experimentais relativos
às áreas, não apresentam distribuição
normal, torna-se necessária a transformação dos dados
pela raíz quadrada dos valores numéricos dos dados realmente
obtidos.
Nessa transformação, o que se faz
de fato é encarar todas áreas calculadas como se fossem quadrados
eqüivalentes ¾ ou seja, com a mesma
área da figura de contorno irregular projetada em gráfico,
figura essa já comentada em parágrafo anterior ¾
de tal forma que a raiz quadrada desses quadrados transformaria uma grandeza
bidimensional (área dos quadrados) em uma grandeza unidimensional,
que seria o comprimento dos lados desses quadrados. Esse tipo de transformação
costuma tornar normal uma distribuição e erros antes não-normal,
porque tende a reduzir a amplitude da variação dos dados
amostrais originais.
Exemplo no.4: variável área (métodos estereológicos).
Um recurso muito prático para calcular áreas,
principalmente de figuras fechadas e de contorno irregular, é o
uso da Estereologia, que basicamente consiste em utilizar uma grade de
pontos com dimensões conhecidas, para calcular a superfície
contida no interior de uma linha de contorno qualquer, a partir do número
de pontos que incidem sobre a superfície fechada que está
sendo avaliada.
É evidente que, quanto maior for a área
da figura, tanto maior será a probabilidade de um número
maior de pontos da grade caírem dentro dela. Na verdade, há
uma proporcionalidade matemática entre o número de pontos
que recaem no interior da figura e a sua área real. Assim, esta
pode ser calculada por comparação com a superfície
total da grade de pontos utilizada, que é uma área conhecida
e representa, em termos de dimensão real, 100 % da área da
grade de pontos, traduzidos pelo número total de pontos nela contidos.
A grade de pontos pode ser adaptada à ocular
de um microscópio, ou opcionalmente traçada em papel, projetando-se
sobre este a imagem microscópica da área que se quer medir,
por meio de uma câmara clara. Este segundo método tem a vantagem
de possibilitar a contagem de pontos posteriormente, abreviando o tempo
em que o pesquisador fica preso ao microscópio, um processo muitas
vezes cansativo para os olhos.
Um terceiro método consiste em obter slides
das áreas a serem medidas (ou cópias transparentes dessas
áreas), as quais poderão ser aumentadas, pela projeção
das transparências sobre um anteparo, o que permite o emprego de
grades com maior número de pontos, dando maior precisão à
avaliação das áreas, e maior comodidade visual na
contagem de pontos.
Os métodos estereológicos podem ser
empregados também na contagem diferencial de elementos componentes
de uma estrutura qualquer, sejam eles elementos tissulares simples, tais
como células num processo inflamatório ou neoplásico,
sejam estruturas mais complexas, como vasos sanguíneos, trabéculas
ósseas ou fibras colágenas, num processo de cicatrização
de uma ferida qualquer.
Com auxílio dos métodos estereológicos,
caso seja levada em consideração a espessura dos cortes histológicos,
por exemplo, é possível avaliar também o volume das
estruturas estudadas, aparentemente a partir de imagens tomadas em duas
dimensões. São portanto métodos extremamente úteis,
porque permitem ao pesquisador transformar em valores numéricos
algo que é basicamente de natureza qualitativa, e não quantitativa,
como é o caso dos cortes histológicos. Esse mesmo recurso
estereológico foi utilizado no artifício técnico descrito
a seguir.
Exemplo no.5: transformação de áreas em vetores.
Além dos quadros histológicos, as radiografias
são também exemplos de quadros cuja natureza é basicamente
qualitativa. O autor destas linhas já teve em mãos um caso
em que os resultados do trabalho de pesquisa de um pós-graduando
consistiam numa série de radiografias da articulação
temporomandibular (ATM). Quando me procurou, travamos o seguinte diálogo:
¾ E agora, professor,
o que faço com os resultados da minha pesquisa?!, perguntou-me,
completamente desarvorado.
Examinei uma das radiografias contra a luz, e perguntei,
por meu turno:
¾ Você se
lembra de uma coisa que aprendeu no colegial (ou mesmo no cursinho para
o vestibular) chamada números complexos?
¾ Não me
lembro, confessou-me ele, sem saber aonde eu queria chegar.
¾ Mas eu me lembro,
repliquei, e é exatamente o fato de me lembrar que vai resolver
o seu problema...
¾ O que vem a
ser número complexo, professor?
¾ Talvez você
o conheça pelo nome de número imaginário, representado
por aquele i usado em equações de segundo grau quando, após
a aplicação da fórmula de Bhaskara, resultam raízes
quadradas de números negativos. Por exemplo, a raiz de – 4, que
é transcrita como ±2i. O número é dito imaginário
porque não há raíz quadrada de números negativos,
uma vez que qualquer número positivo ou negativo, quando elevado
ao quadrado produz apenas números positivos.
¾ E como posso
reconhecer um número complexo?
¾ A forma geral
de um número complexo é n = a + bi, onde n é um número
complexo qualquer, a e b são números reais, e i é
a raiz quadrada de –1 , ou seja:
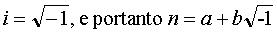
¾ Mas o que tem
isso a ver com as minhas radiografias?!
¾ Tem tudo a ver.
Se você aplicar o teorema de Pitágoras, usando os valores
de a e b, terá a amplitude do deslocamento do côndilo de sua
posição central; e se dividir b por a, terá a tangente
do ângulo em que esse deslocamento se deu. Para saber que ângulo
é esse, basta consultar uma tabela da função tangente.
¾ E como consigo
esses valores de a e b?
¾ Precisamos criar
um método para obter esses valores, e nada melhor do que criar dois
vetores para representá-los.
Eu julgava estar esclarecendo o assunto, mas ele
parecia cada vez mais confuso. Na verdade, eu ainda não imaginara
o método, mas já estava pensando nele exatamente naquele
momento ¾ e ele me surgiu por inteiro,
de um instante para o outro: bastaria criar dois índices estereológicos,
um horizontal e um vertical, e usá-los à guisa de vetores,
como se fossem um sistema vetorial com dois deslocamentos ortogonais, do
qual se determinaria a resultante, calculando-lhe o módulo e o ângulo
de inclinação correspondentes.
A maneira como isso foi feito é bastante
simples:
Primeiramente, selecionaram-se dois pontos de referência
anatômicos cuja posição fosse relativamente estável
nas radiografias da ATM, ou seja, que variasse pouco, em função
de pequenas variações decorrentes do ângulo de incidência
dos raios-x. Os pontos de referência escolhidos foram a imagem do
meato auditivo externo e a crista anterior da cavidade articular da ATM.
Em seguida, por meio de um projetor comum de slides,
projetava-se a imagem da radiografia sobre uma folha de papel presa a um
anteparo vertical plano, colocado sempre à mesma distância
do projetor, para que a ampliação fosse sempre a mesma em
todas as radiografias, e traçava-se a lápis o contorno do
côndilo, da cavidade articular e do conduto auditivo.
Uma vez obtido o desenho ampliado da ATM (com os
pontos de referência citados nos itens anteriores), traçavam-se
seis linhas retas sobre esse desenho, sendo três verticais e três
horizontais.
A linha básica horizontal era uma reta que
tangenciava ao mesmo tempo a crista da parede anterior da cavidade articular
da ATM e a borda inferior do meato auditivo. As outras duas retas horizontais
eram paralelas a essa linha básica, e tangenciavam respectivamente
o contorno superior da cabeça do côndilo e o contorno da cavidade
articular em seu ponto mais elevado.
A linha básica vertical era uma perpendicular
à linha básica horizontal, e passava sobre o ponto em que
esta tangenciava o contorno do côndilo. As outras retas verticais
eram paralelas a essa vertical básica e passavam sobre os ponto
de interseção da linha básica horizontal com o contorno
da cavidade articular, sendo portanto um anterior e outro posterior a essa
linha vertical básica.
Desse modo, as seis linhas assim traçadas
delimitavam uma área retangular subdividida em quadrantes, sendo
dois destes superiores e dois inferiores, e ao mesmo tempo dois anteriores
e dois posteriores, conforme considerados no sentido vertical ou horizontal
do desenho.
Sobre esse esboço da ATM era colocada uma
grade de pontos, e contados os pontos que incidiam em cada um dos quadrantes.
A soma do número de pontos contidos nos dois quadrantes superiores,
dividida pela soma do número de pontos incidentes sobre os dois
quadrantes inferiores, fornecia o valor do vetor vertical do sistema vetorial
buscado.
Da mesma forma, a soma dos pontos contidos nos dois
quadrantes anteriores, dividida pela soma dos pontos referentes aos dois
quadrantes posteriores, fornecia o valor do vetor vertical desse sistema
vetorial. Esses dois valores numéricos eram, em suma, o a e o b
procurados para definir o número complexo que caracterizava cada
uma das radiografias da ATM, que eram assim transformadas em valores núméricos,
o que as tornava passíveis de uma análise estatística
coerente, que antes parecia uma tarefa tecnicamente irrealizável.
E assim foi feito...
Uma observação interessante sobre
o método acima descrito é que, quando o número de
pontos contidos nos quatro quadrantes é exatamente o mesmo em todos
eles, isso resulta em dois vetores iguais a 1, que teoricamente deveria
representar a posição centrada do côndilo no interior
da cavidade articular. Entretanto, o cálculo do módulo do
vetor resultante revela que essa posição, dada pela raiz
quadrada de 1² + 1² (Ö2), é
igual a 1,4241356, e não 1 ou 0, como se poderia pensar. Da mesma
forma, o ângulo cuja tangente é igual a 1 é o de 45°,
e não 0°... Assim, todos os deslocamentos do côndilo deverão
ser estudados em relação a esses valores referenciais teóricos,
a fim de se avaliarem corretamente os valores reais desses desvios de posição
(extensão e angulagem).
Exemplo no.6: a probabilidade binomial como variável.
Outro caso curioso envolvia o emprego do teste bacteológico
conhecido como BANA. A pós-graduanda, autora do trabalho, dividia
cada arcada dentária em três regiões, sendo duas posteriores
e uma anterior, o que resultava na divisão das duas arcadas em seis
sextantes. De um dente pertencente a cada um desses sextantes, colhia-se
uma amostra do conteúdo de bolsas periodontais ali existentes, e
com esse material realizadvam-se os testes bacteriológicos, que
poderiam dar resultados exclusivamente positivos (+) ou negativos (-).
O projeto inicial de trabalho previa a contagem
e a comparação do número de resultados positivos nos
dois grupos estudados, que reuniam pacientes diabéticos do tipo
I (insulino-dependentes) e do tipo II (não-insulino-dependentes).
Tudo estaria bem, não fossem dois detalhes, dos quais a autora do
trabalho aparentemente não se dera conta ao planejar sua pesquisa.
a) O primeiro desses detalhes dizia respeito ao fato de nem sempre
os seis sextantes estarem presentes, uma vez que muitos pacientes eram
parcialmente desdentados, o que fazia variar o número de sextantes,
e conseqüentemente o número de testes, por paciente. Essa variabilidade
do número total de testes por paciente desaconselhava a contagem
pura e simples do número de resultados positivos do teste BANA,
uma vez que dois casos positivos em três testes realizados, por exemplo,
não significam a mesma coisa que quatro, cinco ou seis casos positivos
obtidos em seis testes realizados.
Para resolver o problema, sugeri um artifício
estatístico que não me consta ter sido usado jamais por alguém
anteriormente: adotar a probabilidade binomial de, em n testes realizados,
serem obtidas m respostas positivas (+); ou afirmativas, caso a variável
inicial consistisse em respostas afirmativas (sim), ou negativas (não).
Com essa mudança de variável, os dados
numéricos deixavam de ser valores discretos, que podiam ser apenas
contados, produzindo freqüências que variavam de 0 a 6, para
se transformarem em grandezas contínuas, que variavam de 0 a 1,
que é a variação da probabilidade, ou de 0 a 100,
se essas probabilidades fossem transformadas em probabilidades percentuais,
uma escolha que, em termos estatísticos, é totalmente indiferente.
E assim foi feito, com o mais absoluto sucesso.
Para aqueles que possam algum dia ter diante de
si o mesmo problema, transcrevemos abaixo a equação utilizada
para efetuar a transformação das freqüências de
respostas + e - (ou sim e não) em probabilidades de ocorrência
dessas freqüências em n número de casos:
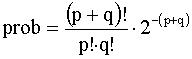
onde q = número de respostas negativas (-), e p = número
de respostas positivas (+).
b) O segundo detalhe acima mencionado, que entrevi logo de início
no plano de pesquisa ora comentado, envolvia um problema talvez bastante
comum entre os pesquisadores: a escolha do grupo controle, principalmente
quando, como no caso focalizado, duas condições patológicas
estão simultaneamente presentes no mesmo paciente, e se deseja estudar
uma delas exatamente em função da presença concomitante
da outra.
Nesse caso, convém que o grupo controle não
seja formado por indivíduos sadios, mas sim por pessoas portadoras
de apenas uma das condições patológicas estudadas,
para que se possam avaliar convenientemente os efeitos da outra sobre esta,
que os pacientes controles também apresentam. No caso da associação
diabetes/doença periodontal, é evidente que o interesse maior
concentra-se nesta última, e que aquilo que se quer verificar é
de que maneira os dois tipos diferentes de diabetes poderiam influir no
desenvolvimento, ou no agravamento, da condição periodontal.
Assim, o ponto de referência (grupo controle)
seria representado por pacientes não-diabéticos, porém
igualmente portadores de doença periodontal, mesmo porque já
está perfeitamente estabelecido que os pacientes diabéticos
tendem a desenvolver doença periodontal, mais cedo ou mais tarde,
de modo que é sempre mais fácil encontrar pacientes não-diabéticos
com doença periodontal, do que achar pacientes diabéticos
sem doença periodontal.
Exemplo no.7: escores, uma variável que se deve evitar
(sempre que possível).
Tenho tanta fé nos escores, como variável
capaz de avaliar um fenômeno qualquer, como tenho nas notas de avaliação
como meio eficaz para julgar o desempenho de um aluno na escola. Tanto
aqueles como estas implicam um grau de subjetividade que é sempre
grande demais para o gosto de um estaticista. Os estaticistas, de um modo
geral, preferem tratar com variáveis que sejam mais objetivas do
que uma simples opinião pessoal, a qual nunca possui a imparcialidade
fria de um instrumento de medida.
De fato, a opinião humana, por melhor que
seja o avaliador, é sempre mais sujeita a falhas de interpretação
do que um instrumento de medida, seja este qual for e seja qual for o seu
grau de precisão. Em termos puramente estatísticos, isso
quer dizer que a variabilidade da opinião humana tende a aumentar
o valor do erro experimental, o que conduz fatalmente a uma redução
na capacidade de julgamento de pequenas diferenças entre as grandezas
comparadas.
Realmente, é preciso ter sempre em mente
que a significância estatística é a conseqüência
direta de uma divisão de variâncias; ou seja, uma fração
ordinária na qual o numerador (ou o dividendo) é a variância
observada entre as grandezas comparadas, e o denominador (ou o divisor)
é a variância entre as repetições (ou seja,
a variância do erro experimental). Ora, se o denominador da fração
for demasiadamente grande, o quociente da divisão será pequeno
demais: e se for pequeno demais, o quociente será demasiadamente
grande. Em qualquer das alternativas, o resultado estará prejudicado,
produzindo falsas não-significâncias no primeiro caso, e falsas
significâncias no segundo. Por isso, o erro tem de ser razoável,
nem exageradamente pequeno, nem desmesuradamente grande. Os escores tendem
a produzir erros experimentais grandes demais, no caso de avaliadores determinados
aleatoriamente; e pequenos demais, no caso dos avaliadores ditos calibrados.
Do ponto de vista estatístico, um resultado
significante, no caso de erros experimentais grandes demais, seria altamente
confiável, uma vez que revelou significância mesmo com o tamanho
do erro experimental trabalhando contra. Todavia, o mesmo não se
poderia dizer com relação aos resultados não-significantes,
que poderiam caracterizar aquilo que se convencionou chamar de falsos negativos.
Neste caso, a diferença entre os grupos comparados estaria sendo
mascarada pelas diferenças muito grandes encontradas entre as próprias
repetições realizadas dentro de cada grupo. Tecnicamente,
em jargão estatístico, se diria que a variação
entre grupos seria mais ou menos igual à variação
intra-grupo ¾ e é exatamente essa quase-igualdade que caracteriza
a não-significância estatística.
O raciocínio expresso no parágrafo
anterior vale também para o caso de resultados não-significantes,
em caso de erros experimentais demasiadamente pequenos. Neste caso, os
resultados seriam válidos para a não-significância,
mas poderiam acarretar erros nos casos de significância (falsos positivos).
A razão é basicamente a mesma já
exposta no parágrafo referido: a significância aparente correria
por conta apenas da divisão de uma variância relativamente
grande entre grupos por uma variância intra-grupo inadequada exatamente
por ser pequena demais. Seria como querer avaliar a variação
do tamanho de melancias tomando como base a variação do tamanho
de jabuticabas. Haveria, nesse caso, incompatibilidade entre o objeto medido
e a unidade de medida utilizada É por esse motivo, exatamente, que
se mede tecido em metros, estrada em quilômetros, e célula
em micrometros.
Contudo, por uma questão de coerência,
devo observar que aquilo que foi dito acima traduz também apenas
uma opinião pessoal do autor destas linhas, com tudo que uma opinião
pessoal possa implicar, de acordo com o próprio texto em que essa
opinião foi exposta. Aliás, o próprio Cristo já
prevenia seus apóstolos contra o perigo do julgamento humano, quando
sabiamente ensinou: "Não julgueis, para não serdes julgados,
pois com o julgamento com que julgais sereis julgados, e com a medida com
que medis sereis medidos" (Mateus, 7:1-2).
Apesar do risco, todavia, não posso deixar
de expressar minha opinião, e estou disposto a agüentar o tranco
que disso advier. Mesmo porque o ensinamento do Mestre apenas confirma
essa opinião: aquele que usa escores deve estar também preparado
para enfentar as conseqüências dos erros de julgamento de seus
avaliadores.
O diabo (como provavelmente diria o próprio
Criador) é que às vezes não há como evitar
usá-los, porque a natureza do experimento pode tornar incontornável
o seu emprego na avaliação experimental... Mas, pelo amor
de Deus!, se o uso de escores for inevitável, jamais calibrem os
seus avaliadores, porque isso tornaria a coisa ainda pior!
Uma observação final sobre os escores:
evitem o escore 0 (zero). Procurem começar com o escore 1 para indicar
a ausência seja lá do que for. Como a gradação
é uma classificação meramente convencional, isso pode
ser feito sem nenhum problema. O grau 0 não esclarece coisa alguma,
mas pode acarretar alguma dificuldade, em caso de divisão por 0,
ou se houver necessidade de transformação logarítimica
dos dados.
Aproveitando o ensejo, deve-se, tanto quanto possivel,
evitar dados com valores negativos, porque eles poderiam complicar as coisas
em caso de ser necessário extrair a raiz quadrada desses valores
negativos. Os zeros e os valores negaivos não são dificuldades
incontornáveis, quando presentes, mas a sua inexistência pode
poupar tempo ao investigador, quando do tratamento estatístico dos
dados obtidos em sua pesquisa.
Exemplo no 8: uso e abuso.
Da variável porcentagem.
O principal, e provavelmente o mais comum dos abusos
e das liberdades que se tomam com a variável porcentagem, talvez
consista em usá-la para números de dados inferiores a 100.
De fato, esse procedimento raia pelos domínios da profecia, ou da
adivinhação, uma vez que, a partir de um número reduzido
de dados, pretende-se extrapolar freqüências e achados, observados
em amostras reduzidas, para amostras de tamanho igual ou maior que 100,
amostras estas não existentes, e que podem não vir a apresentar
as mesmas características dos dados que já foram obtidos
até aquele momento, podendo na verdade fugir completamente a essas
características, uma vez que porcentagens atuais não garantem
porcentagens iguais no futuro.
Porcentagens são portanto dados que falam
de fatos passados, e não de fatos que ainda não aconteceram.
Quando se diz tantos por cento, o que se quer dizer é que para cada
grupo de cem dos dados (que já se tem em mãos) uma certa
parte tem uma determinada característica, dentre as que se estão
estudando. Nada garante que o dobro do número desses dados virá
a apresentar o dobro dessa freqüência.
Em caso de amostras pequenas, é preferível
falar em proporção, e não em porcentagem. Por exemplo:
6 casos em 36 estudados (6 / 36 = 0,167). A porcentagem seria essa mesma
proporção multiplicada por 100 (16,67%), mas só teria
sentido se se tratasse de 60 em 360 dados, ou, na pior das hipóteses,
de 17 em 100 para a mesma porcentagem.
(Falta escrever) A transformação
angular.
Exemplo no10: as variáveis multidimensionais.
Raciocínio idêntico ao apresentado no
Exemplo no4 pode ser feito em relação a variáveis
tridimensionais, das quais o volume é o exemplo representativo mais
simples. A raiz cúbica dos dados transforma essa grandeza tridimensional
e uma grandeza unidimensional, que seria o comprimento da aresta de um
cubo, mesmo que o volume inicial não seja exatamente um cubo, mas
uma esfera, um elipsóide, ou um sólido sem forma definida,
mas cujo volume pode ser medido. Qualquer que seja o sólido, o valor
do seu volume pode ser transformado numericamente em um valor equivalente
ao de um cubo com uma aresta de comprimento x, aresta essa que, elevada
ao cubo, reproduz o volume tanto do próprio cubo como do volume
do sólido inicialmente considerado. Nesse caso, o tratamento estatístico
pode ser feito considerando as arestas dos diversos cubos de volumes equivalentes
aos dos sólidos originais, independentemente da forma real destes.
(Abaixo estão os itens que faltam ainda
para escrever:)
Resumos dos testes que constam no software
GMC
Exemplo no. 9: o denominador comum nas comparações.
Número suficiente de dados da amostra.
Como calcular? |