A esta altura de nossas considerações, a variável e os fatores de variação já foram identificados, o tipo de variável foi reconhecido, e a tabela de dados construída e preenchida com os dados obtidos na fase experimental. E agora? O que fazer com essa tabela e com os dados numéricos nela contidos?

Pequeno retrospecto das fases iniciais

    Ficou dito, em capítulos anteriores, que o tratamento estatístico deve ser cogitado já nos primórdios da pesquisa, quando ainda se está na elaboração do seu projeto inicial, ou mesmo durante a fase de execução do plano-piloto dos experimentos. De fato, há muita coisa que já pode ser pensada e estudada nessas fases iniciais, em termos de tratamento estatístico dos dados. Porém há também outros detalhes que somente podem ser considerados após ter em mãos os dados numéricos colhidos nos ensaios. Entre as coisas que podem ser verificadas ainda na fase inicial da pesquisa está a vinculação, ou independência, dos dados experimentais, mas o conhecimento desse pormenor ainda não é tão relevante a essa altura do desenvolvimento da pesquisa, ou de seu tratamento estatístico. Mas se-lo-á mais adiante, ocasião em que o assunto será abordado novamente, tecendo-se então sobre ele considerações mais elaboradas.

A distribuição dos erros experimentais

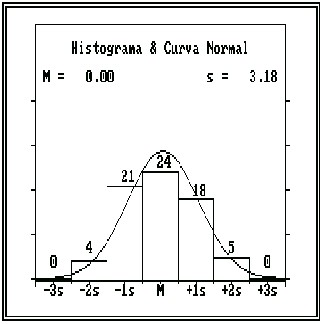
    Muito mais importante, todavia, seria analisar agora a distribuição de freqüências dos dados experimentais; ou, mais apropriadamente, estudar a maneira como os erros desses dados se distribuem em torno da média. Enfim, é preciso saber se a distribuição dos erros experimentais em torno da média é normal, ou seja, se o seu histograma de freqüências segue a configuração geral da curva matemática conhecida como curva normal.
    Mas... poderão perguntar os eventuais leitores deste texto, por que isso seria assim tão importante? A resposta é: porque os primeiros testes estatísticos, talvez os mais importantes de quantos foram desenvolvidos pelos estudiosos, tiveram por premissa que a distribuição dos erros deveria ser normal, ou seja, que ela deveria ter uma distribuição de freqüências semelhante à da curva de Gauss, também chamada curva normal ou curva dos erros.

Por que curva "normal"?

    A denominação curva de Gauss explica-se porque foi esse notável matemático alemão quem encontrou a sua equação matemática. Da mesma forma, a expressão curva dos erros também se justifica, porque Gauss deduziu a sua equação matemática precisamente a partir de estudos realizados sobre a distribuição dos erros de medida em torno da média, ou seja, a lei matemática que regia a dispersão e o afastamento dos valores de medida em relação ao seu valor médio; ou, mais exatamente, em relação ao valor real da grandeza medida. Sim, tudo isso é compreensível. Mas por que essa curva seria chamada normal?
    Na verdade, eu não sei nem nunca li qualquer explicação racional para isso. Acredito, porém, que essa denominação tenha algo a ver com os fenômenos naturais, tal como ocorre com outras curvas matemáticas, que traduzem fenômenos normalmente encontrados na natureza. É o caso, por exemplo, da curva chamada catenária (do latim catena = cadeia, corrente), cuja equação expressa matematicamente a curva natural descrita por uma corrente metálica, quando presa pelas extremidades e submetida à ação do próprio peso.
    Agora, caros leitores, mentalizem, por exemplo, uma ampulheta e pensem: qual seria a equação matemática que descreve o perfil do montículo de areia que flui dentro dela e se deposita no seu compartimento inferior? Ou qual seria a equação matemática capaz de descrever o perfil do montículo que se forma, quando se despeja sobre o solo um saco de grãos de um cereal qualquer? Eu pessoalmente estou convencido de que, muito provavelmente, seria uma curva dessa família de curvas conhecidas como curvas normais. Talvez derive daí a denominação normal atribuída a esse tipo de curva.